Maximum Martin - Unpacking Big Ideas And Thrilling Stories
When we talk about "maximum martin," it turns out we are looking at a couple of really interesting, yet quite different, ideas. It's like, you know, finding two separate paths that just happen to share a similar sounding signpost. On one hand, there's a deep concept from the world of mathematics, something called Martin's Maximum, which deals with very big numbers and how we think about them.
Then, on the other hand, there's a whole different kind of "maximum martin" that brings to mind exciting tales and gripping suspense. This involves a well-known writer and her popular series of books, which are packed with mystery and action. It's pretty cool how one phrase can point to such varied subjects, isn't it? So, we'll explore both sides of this idea, pulling details straight from what's been said about them.
This piece will take a look at these distinct meanings, from the abstract ideas of set theory to the thrilling stories found on bookshelves. We will try to make sense of what each "maximum martin" is all about, using just the information that has been put forward. It's a bit like, in a way, exploring different kinds of adventures, each with its own kind of excitement.
- Madelyn Cline Boyfriend
- Hally Holston
- Kristen Stewart Girlfriends
- Lee Sung Kyung Dating
- Natalie Morales Actress Relationships
Table of Contents
- Kat Martin - A Storyteller's Reach
- What is Martin's Maximum in Set Theory?
- The "Maximum Security" World of Kat Martin
- What About SS Maximus Martin?
Kat Martin - A Storyteller's Reach
Let's first talk about Kat Martin, a writer who has made quite a name for herself. She is known for creating stories that grab your attention and keep you hooked. People often call her a New York Times bestselling author, which means a lot of folks enjoy reading what she writes. She has a way with words, a sort of quick and lively style when it comes to telling her tales, so.
Her writing has gained praise from other well-known authors, like Linda Lael Miller, who is also a number one New York Times bestselling author. Linda Lael Miller has said that she really loves Kat Martin's books, pointing out her fast pace when it comes to spinning a yarn. This kind of praise really shows how much people appreciate her work, you know.
Kat Martin has a series that's quite popular, called the "Maximum Security" series. This collection of books has brought her back with some of her most exciting stories yet. For instance, "The Perfect Murder" is one of the thrillers in this group. It's the kind of book that fans of other suspense writers, like Sandra Brown or Linda Howard, might find themselves really enjoying, too it's almost.
- Tahnee Welch Husband
- Is Maria Genero Married
- Rick Moranis Wife
- Alison Doody Husband
- Justin H Min Relationships
Kat Martin's Personal Details
Here is a little bit about Kat Martin, based on the information available:
| Known For | New York Times Bestselling Author |
| Series | Maximum Security Series |
| Style | A quick hand when it comes to storytelling |
What is Martin's Maximum in Set Theory?
Now, let's shift gears to a very different kind of "maximum martin." This one comes from the deep study of mathematics, specifically a field called set theory. Martin's Maximum, often shortened to 'mm', is a powerful idea, a kind of rule or principle, that helps mathematicians figure out things about very large collections of numbers. It's pretty much a big concept in that world, you see.
This idea, Martin's Maximum, has a special connection to something called a "ccc notion of forcing." This is a method that helps keep certain groups of items, known as "stationary subsets of omega one," from changing their place or arrangement. It means that when you use this particular way of making things happen, these special collections stay exactly where they are supposed to be, which is pretty neat.
Martin's Maximum is seen as a very broad type of "forcing axiom" for which things can still make sense. It means it covers a wide range of situations where such a rule can be applied without causing contradictions. This idea has been shown to fit in with other big mathematical concepts, especially when you consider the existence of a "supercompact cardinal," which is a really, really big kind of number, arguably.
It has been proven that this idea is consistent, meaning it doesn't lead to logical problems, if we assume there's a supercompact cardinal, which is a very large number. This was shown in some academic papers, for example, in one known as [22]. So, it's a concept that holds up when you think about these incredibly vast numbers, in a way.
There's also a revised way of doing things, called a "countable support forcing iteration," which helps show that Martin's Maximum can be consistent with a supercompact cardinal. This process leads to a situation where the size of the continuum, often written as 'c', turns out to be the same as 'aleph two' (ℵ2) and also the same as that supercompact cardinal 'kappa' (κ). This is quite a specific mathematical outcome, apparently.
A very interesting aspect of this forcing method is that it does not change the way the "continuum function" behaves for numbers that are at or above that supercompact cardinal 'kappa'. The continuum function describes how many real numbers there are, and this particular method keeps those values fixed for the very large numbers, which is kind of important.
In some respects, Martin's Maximum, especially a stronger version called Martin's Maximum++, has been shown to lead to another important idea in set theory: Woodin's Pmax axiom, also known as (*). This connection is pretty significant because it answered a long-standing question from the 1990s. It also brings together two very important rules of set theory, both of which suggest that there are 'aleph two' (ℵ2) many real numbers, which is quite a lot, basically.
A section of a paper, "Martin's Maximum, Part I, Section 3," briefly explains different versions of another idea called Martin's Axiom (MA) that fit with the Continuum Hypothesis (CH). It also touches on findings by mathematicians Shelah and Woodin, who showed that there isn't a neat, organized inner structure that contains a supercompact cardinal. This is a subtle but important point in their work, you know.
Some weaker forms of Martin's Axiom have also been shown to fit with other ideas, according to joint findings by the authors. This suggests that even less strong versions of these mathematical rules can still make sense within the broader framework of set theory. It's about finding out what fits together logically, still.
The consistency of Martin’s Maximum, or 'mm,1(k)', depends on a certain class of mathematical tools. These tools are called "partial orders p." When you use these tools in a particular way, they make sure that the "stationarity" of all "stationary subsets" stays exactly as it is. This is a very specific condition about how these mathematical operations work, so.
The rule of Martin's Maximum is known to be the strongest possible in a certain sense. This means that another rule, 'fa,1(fpg)', just doesn't work if you use any "forcing notion p" that messes up some of those stationary subsets. It's like, it's the top of the heap when it comes to these kinds of mathematical rules, pretty much.
The people who wrote about this concept have put forward what they say is the strongest form of Martin's Axiom, giving it the name Martin's Maximum. They also showed that this very strong version of the idea is consistent, meaning it holds together logically without problems. This was a big step in understanding these complex mathematical ideas, you know.
How Does Martin's Maximum Affect Numbers?
So, how does this idea of Martin's Maximum actually change our view of numbers, or rather, what does it tell us about them? Well, it mainly tells us about the sheer count of real numbers that exist. Both Martin's Maximum++ and Woodin's Pmax axiom, which are connected, point to the same outcome: there are 'aleph two' (ℵ2) many real numbers. This is a specific, rather large quantity, you see.
It helps to settle questions about the size of infinite sets, especially the set of real numbers. The fact that it doesn't change the "continuum function" for numbers at or above a supercompact cardinal means it offers a very precise way to think about how these vast collections behave. It's a way of pinning down certain properties of numbers that are otherwise quite hard to get a handle on, in a way.
This is quite important for mathematicians who study the foundations of numbers. It provides a framework for how certain very large sets behave, and how they relate to each other. It's like, it gives a clearer picture of the structure of the mathematical universe, especially when you're dealing with infinities, actually.
The "Maximum Security" World of Kat Martin
Now, let's switch back to the other kind of "maximum martin," the one found in the pages of thrilling books. Kat Martin's "Maximum Security" series is a collection of exciting stories that keep readers on the edge of their seats. The series includes titles like "Come Midnight," "Perfect Murder," "Before Nightfall," "Ultimate Betrayal," "The Conspiracy," "The Deception," "Shadows at Dawn," "Wait Until Dark," and "After the Sunrise." That's quite a list, so.
This series is quite extensive, with plans for eight books in total, split between four shorter stories (novellas) and four longer, more substantial books (hardcovers). It's a big project from a writer who clearly loves to tell a good story. Fans of other suspense authors, like Sandra Brown, Linda Howard, and Julie Garwood, are often drawn to these tales, finding a lot to enjoy in them, too it's almost.
"After the Sunrise" is a short story that acts as an introduction to the "Maximum Security" series. It gives readers a little taste of what's to come, and it also includes a
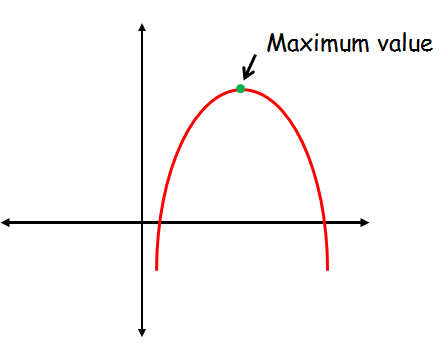
Maximum or Minimum Value of a Quadratic Function
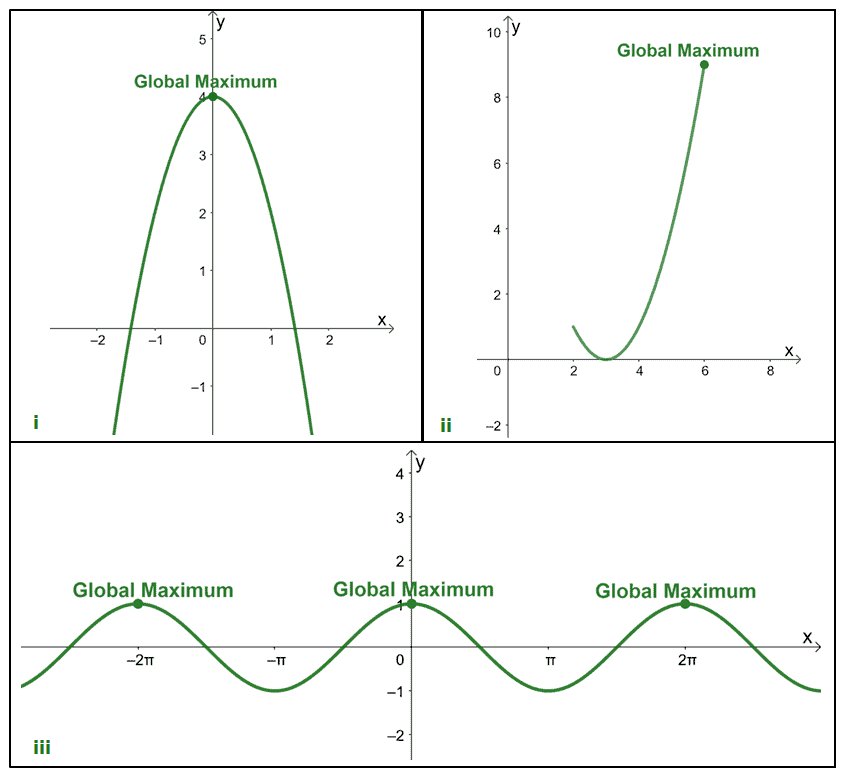
Absolute maximum - Definition, Conditions, and Examples
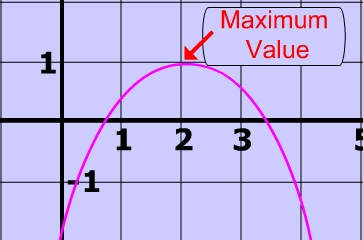
Presentation Name on emaze